Xác suất thống kê-Tổng hợp công thức xác suất

Vì không có các phần tử bị trùng, nên ta được phép cộng như phép cộng thông thường.

$$P(A+B)=P(A)+P(B)$$

Công thức xác suất có điều kiện

Xác suất có điều kiện là xác suất A sẽ xảy ra khi biết B đã xảy ra. Ký hiệu:

$$P(A|B)$$

Giả sử: Tính xác suất A xảy ra khi biết B xảy ra. Tức là phần tô màu xám.

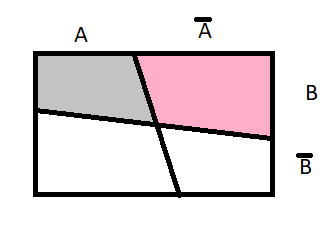
Nhìn hình trên, bạn có thể tự suy ra được công thức không?

Rất đơn giản, tập vũ trụ hiện tại bị thu hẹp lại còn tập B thôi. Nên ta tính xác xuất như cách chúng ta hay làm là lấy biến cố chia tập vũ trụ (hiện tại là tập B).

$$P(A|B)=\frac{P(AB)}{P(B)}$$

* Các bạn lưu ý, $P(A|B) != P(AB)$ nhé. Vì $P(A|B)$ tập vũ trụ là B, nhưng $P(AB)$ tập vũ trụ là $\upsilon$.

Công thức nhân

Vậy đã có công thức tổng, thì phải có công thức nhân đúng không? Mình cố tình trình bày công thức xác suất có điều kiện trước để làm tiền đề cho phần trình bày công thức nhân này. Với công thức trên, bạn hoàn toàn có thể suy ra được công thức nhân.

$$P(AB)=P(A|B)P(B)$$

Nhiều bạn thắc mắc, thế công thức này có phải công thức nhân không: $P(AB)=P(A)+P(B)-P(A+B)$ từ công thức cộng suy ra. Tất nhiên là không :), vì nó là công thức cộng, toàn dấu cộng thế kia mà :). Lưu ý không nhầm lẫn nha.

Để hiểu công thức này, mà không cần nhớ thì bạn đọc ví dụ sau:

Giả sử lớp học có 100 người, chia làm 2 nhóm. Nhóm A có 10 học sinh giỏi và 0 học sinh trung bình khá, nhóm $\bar{A}$ có 0 học sinh giỏi và 90 học sinh trung bình, khá. Gọi B là biến cố có học sinh giỏi. Ta nhìn vào sơ đồ sau:

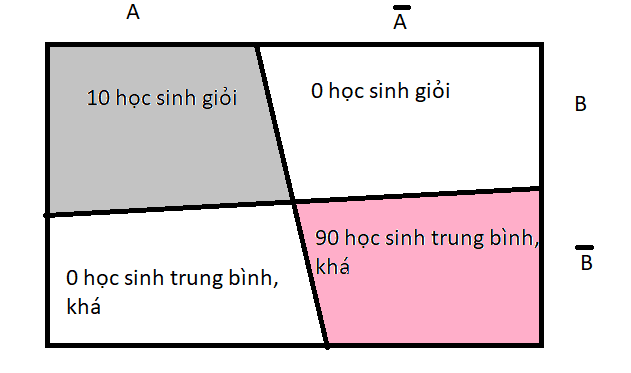
Vậy số xác suất chọn được học sinh ở nhóm A khi biết là học sinh đó giỏi là bao nhiêu? Tức là, bạn đã chọn ra được 1 bạn là học sinh giỏi rồi, giờ bạn tính xác suất bạn đó ở nhóm A hay $\bar {A}$ mà thôi. Không cần nhìn hình, cũng biết được xác suất là $100%$ rồi. Đây là kết quả của $P(A|B)$.

$P(AB)$ đâu? Bây giờ, đi giải nghĩa $P(AB)$ là gì trước đã. $P(AB)$ là xác xuất để chọn được học sinh ở nhóm A và là học sinh giỏi.

Bây giờ, xem lại chúng ta đã có những gì? $P(A|B) = 1, P(A)=0.1, P(\bar {A})=0.9, P(B)=0.1, P(\bar {B})=0.9$

Vậy $P(AB) = P(A|B)P(B) = 1\times 0.1$, giải thích 100% trong (của) 10% :).

Công thức nhân tổng quát

Ở trên là nhân 2 biến cố với nhau, còn giờ nhân nhiều biến cố với nhau thì như thế nào?

$$P(A_1.A_2.A_3...A_n)=P(A_1|A_2.A_3...A_n).P(A_2|A_3.A_4...A_n)...P(A_n)$$

Để chứng minh bạn cứ thực hiện phép nhân của hai biến cố:

$P(A_1.A_2.A_3...A_n)=P(A_1|A_2.A_3...A_n).P(A_2.A_3...A_n)$

$\Leftrightarrow P(A_1|A_2.A_3...A_n).(P(A_2|A_3.A_4...A_n).P(A_3.A_4...A_n))$

Cứ nhân từ từ thì ra được công thức trên.

Công thức xác suất toàn phần

$$P(B)=P(\overline{A}B)+P(\overline{A}B)=P(B|A)P(A)+P(B|\overline{A})P(\overline{A})$$

Do $\overline{A}B \cap \overline{A}B=\varnothing$. Và $B=\overline{A}B+\overline{A}B$

Công thức xác suất tổng quát toàn phần

$$P(B)=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+...+P(B|A_n)P(A_n)$$

Do $A_1,A_2,A_3,...,A_n$ xung khắc đôi một và $B = A_1B+A_2B+A_3B+...+A_nB$.

Mong rằng qua bài viết này, các bạn có thể áp dụng các công thức vào để rèn luyện.